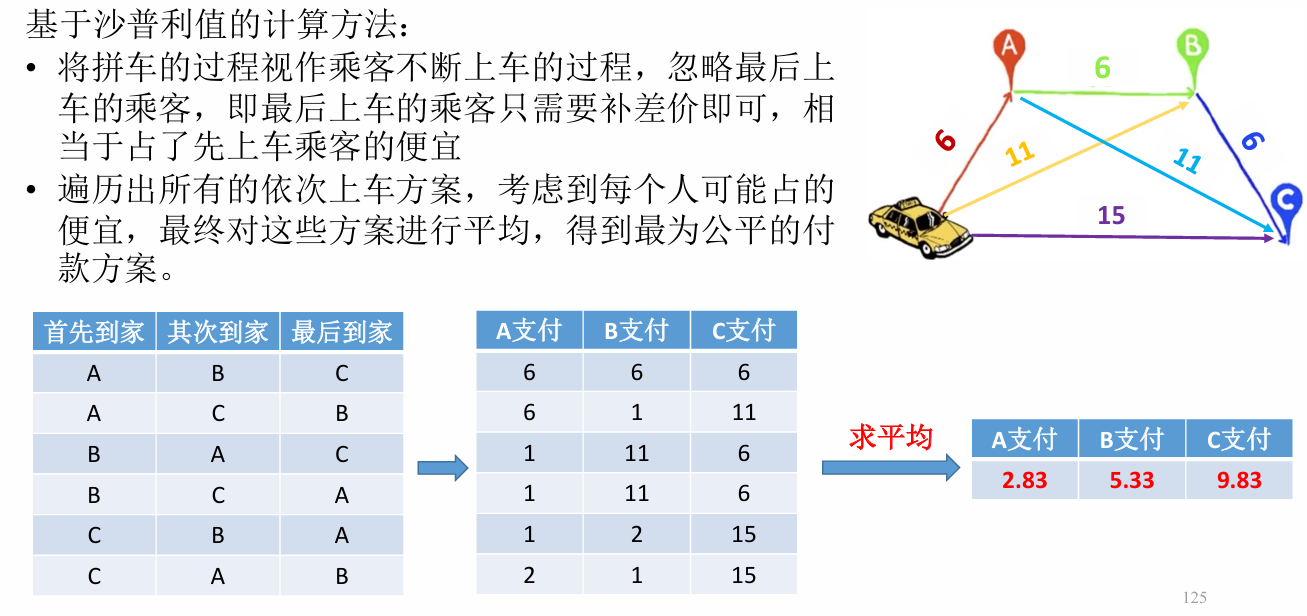
06 强化学习

01 强化学习定义：马尔科夫决策过程

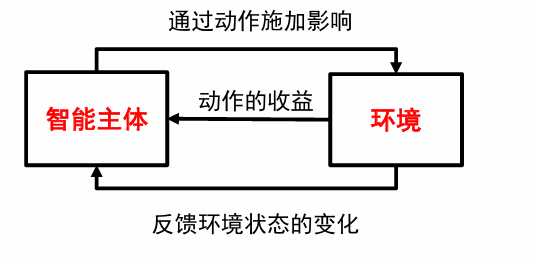
在智能主体与环境的交互中，学习能最大化收益的行动模式：

离散马尔可夫过程 Discrete Markov Process

基本概念

随机过程：是一列随时间变化的随机变量;

当时间是离散量时，一个随机过程可以表示为 ${X_{t}}_{t = 0, 1, 2, \cdot \cdot \cdot}$ , 其中每个 $X_{t}$ 都是一个随机变量，这被称为离散随机过程

马尔可夫链（Markov Chain）：满足马尔可夫性（Markov Property）的离散随机过程，也被称为离散马尔科夫过程

𝒕+𝟏时刻状态仅与𝒕时刻状态相关
二阶：𝒕 +𝟏时刻状态与𝒕和𝒕−𝟏时刻状态相关

马尔可夫奖励过程（Markov Reward Process）：引入奖励

奖励函数 $R : S \times S \mapsto R$ , 其中 $R (S_{t}, S_{t + 1})$ 描述了从第 $t$ 步状态转移到第 $t + 1$ 步状态所获得奖励
在一个序列决策过程中，不同状态之间的转移产生了一系列的奖励 $(R_{1}, R_{2}, \cdot \cdot \cdot)$ , 其中 $R_{t + 1}$ 为 $R (S_{t}, S_{t + 1})$ 的简便记法
为了比较不同的奖励序列，定义反馈 (return), 用来反映累加奖励： $G_{t} = R_{t + 1} + γ R_{t + 2} + γ^{2} R_{t + 3} + \dots$ 其中衰退系数 (decay factor) $γ \in [0, 1]$

马尔可夫决策过程（Markov Decision Process）：引入动作

定义智能主体能够采取的动作集合为 $A$
可以是无限的
由于不同的动作对环境造成的影响不同，因此状态转移概率定义为 $P r (S_{t + 1} | S_{t}, a_{t})$ ，其中 $a_{t} \in A$ 为第 $t$ 步采取的动作
可以是随机概率性的转移
奖励可能受动作的影响，因此修改奖励函数为 $R (S_{t}, a_{t}, S_{t + 1})$

例子

使用离散马尔可夫决策过程描述机器人移动问题：

随机变量序列 ${S_{t}}_{t = 0, 1, 2, \dots}$ : $S_{t}$ 表示机器人第 $t$ 步所在位置（即状态），每个随机变量 $S_{t}$ 的取值范围为 $S = {s_{1}, s_{2}, \dots, s_{9}, s_{d}}$
动作集合: $A = {上, 右}$
状态转移概率 $P r (S_{t + 1} | S_{t}, a_{t})$ : 满足马尔可夫性，其中 $a_{t} \in A$ 。状态转移
奖励函数： $R (S_{t}, a_{t}, S_{t + 1})$
衰退系数： $γ \in [0, 1]$

综合以上信息，可通过 $M D P = {S, A, P r, R, γ}$ 来刻画马尔科夫决策过程

马尔可夫决策过程 $M D P = {S, A, P r, R, γ}$ 是刻画强化学习中环境的标准形式
马尔可夫决策过程可用如下序列来表示：
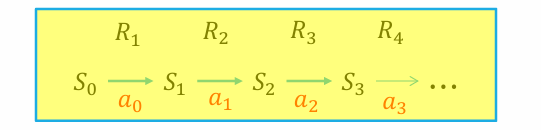
马尔科夫过程中产生的状态序列称为轨迹 (trajectory), 可如下表示 $(S_{0}, a_{0}, R_{1}, S_{1}, a_{1}, R_{2}, \dots, S_{T})$
轨迹长度可以是无限的，也可以有终止状态 $S_{T}$ 。有终止状态的问题叫做分段的 (episodic), 否则叫做持续的 (continuing)
- 分段问题中，一个从初始状态到终止状态的完整轨迹称为一个片段 (episode)

策略学习

智能主体如何与环境交互而完成任务？需要进行策略学习

已知的：S A R $γ$
不一定已知的：Pr
观察到的： $(S_{0}, a_{0}, R_{1}, S_{1}, a_{1}, R_{2}, . . ., S_{T})$

策略函数：

策略函数 $π : S \times A \mapsto [0, 1]$ , 其中 $π (s, a)$ 的值表示在状态 s 下采取动作 $a$ 的概率
策略函数的输出可以是确定的，即给定 s 情况下，只有一个动作 $a$ 使得概率 $π ($ s, $a)$ 取值为 1。对于确定的策略，记为 $a = π (s)$

为了对策略函数𝜋进行评估，定义

价值函数 (Value Function)
$V : S \mapsto R$ , 其中 $V_{π} (s) = E_{π} [G_{t} | S_{t} = s]$
即在第 $t$ 步状态为 s 时，按照策略 $π$ 行动后在未来所获得反馈值的期望 $G_{t} = R_{t + 1} + γ R_{t + 2} + γ^{2} R_{t + 3} + \dots$
动作-价值函数 (Action-Value Function)
$q : S \times A \mapsto R$ , 其中 $q_{π} (s, a) = E_{π} [G_{t} | S_{t} = s, A_{t} = a]$
表示在第 $t$ 步状态为 s 时，按照策略 $π$ 采取动作 $a$ 后，在未来所获得反馈值的期望

这样，策略学习转换为如下优化问题：寻找一个最优策略 $π^{*}$ , 对任意 $s \in S$ 使得 $V_{π}^{*} (s)$ 值最大

价值函数与动作-价值函数的关系——贝尔曼方程（Bellman Equation）

$V_{π} (s) = \sum_{a \in A} π (s, a) q_{π} (s, a)$ $q_{π} (s, a) = \sum_{s^{'} \in S} P r (s^{'} | s, a) [R (s, a, s^{'}) + γ V_{π} (s^{'})]$

02 策略优化与策略评估

强化学习求解：在策略优化和策略评估的交替迭代中优化参数

强化学习的求解方法：

基于价值 (Value-based) 的方法
- 对价值函数进行建模和估计, 以此为依据制订策略
基于策略 (Policy-based) 的方法
- 对策略函数直接进行建模和估计, 优化策略函数使反馈最大化
基于模型 (Model-based) 的方法
- 对环境的运作机制建模,然后进行规划 (planning) 等

基于价值（Value-based）的方法

策略优化

给定当前策略 $π$ 、价值函数 $V_{π}$ 和行动-价值函数 $q_{π}$ 时，可如下构造新的策略 $π^{'}$ , $π^{'}$ 要满足如下条件：

π^{'} (s) = \arccos_{a} q_{π} (s, a) (对 于 任 意 s \in S)

Example

Pasted image 20250529210225.png

策略评估

通过迭代计算贝尔曼方程进行策略评估

动态规划
蒙特卡洛采样
时序差分（Temporal Difference）

动态规划

算法流程

初始化 $V_{π}$ 函数
循环
- 枚举 $s \in S$
$ν_{π} (s) \leftarrow \sum_{a \in A} π (s, a) \sum_{s^{'} \in S} P r (s^{'} | s, a) [R (s, a, s^{'}) + γ ν_{π} (s^{'})]$
直到 $V_{π}$ 收敛

Example

Pasted image 20250529210850.png|450

蒙特卡洛采样

算法流程

选择不同的起始状态，按照当前策略 $π$ 采样若干轨迹，记它们的集合为D
枚举 $s \in S$
- 计算 $D$ 中 s 每次出现时对应的反馈 $G_{1}, G_{2}, \dots, G_{k}$ $V_{π} (s) \leftarrow \frac{1}{k} \sum_{i = 1}^{k} G_{i}$

Example

Pasted image 20250529211034.png|475

时序差分

算法流程

初始化 $V_{π}$ 函数
循环
- 初始化 s 为初始状态
- 循环
  - $a \sim π (s, \cdot)$
  - 执行动作 $a$ , 观察奖励 $R$ 和下一个状态 $s^{'}$
  - 更新 $V_{π} (s) \leftarrow V_{π} (s) + α [R (s, a, s^{'}) + γ V_{π} (s^{'}) - V_{π} (s)]$
  - $s \leftarrow s^{'}$
- 直到 s 是终止状态
直到 $V_{π}$ 收敛

Example

Pasted image 20250529211552.png|475

基于策略（Policy-based）的方法

通过直接参数化策略函数的方法求解强化学习问题；算法需要求参数化的策略函数的梯度，因此这些方法称为策略梯度法

策略函数的参数化可以表示为 $π_{θ} (s, a)$ ，其中θ为一组参数，函数取值表示在状态 s 下选择动作 a 的概率
和 Q 学习的ϵ贪心策略相比，选择一个动作的概率是随着参数的改变而光滑变化的，对算法收敛有更好的保证

假设强化学习问题的初始状态为 $s_{0}$ ，不难定义算法希望达到的最大化目标为：

J (θ) := V_{π_{θ}} (s_{0})

策略梯度定理

如果能够计算或估计策略函数的梯度，智能体就能直接对策略函数进行优化：

\nabla_{θ} J (θ) = \nabla_{θ} \sum_{s} μ_{π_{θ}} (s) \sum_{a} q_{π_{θ}} (s, a) π_{θ} (s, a)

\propto \sum_{s} μ_{π_{θ}} (s) \sum_{a} q_{π_{θ}} (s, a) \nabla_{θ} π_{θ} (s, a)

$μ_{π_{θ}} (s)$ 称为策略 $π_{θ}$ 的策略分布 (这里假设折扣系数 $γ = 1$ )
在持续问题中， $μ_{π_{θ}} (s)$ 为算法在策略 $π_{θ}$ 安排下从 $s_{0}$ 出发经过无限多步后位于状态 $s$ 的概率
在分段问题中， $μ_{π_{θ}} (s)$ 为归一化后的算法从 $s_{0}$ 出发访问 s 次数的期望。
当 $γ \in (0, 1)$ 时，则需要给每个状态的 $μ_{π_{θ}} (s)$ 值加上一个权重
- 为了简化说明，下文在进行公式推导时始终假设 $γ = 1$

基于蒙特卡洛采样的策略梯度法：REINFORCE

算法只需根据策略来采样一个状态 s、一个动作 a 和将来的轨迹，就能构造公式中求取期望所对应的一个样本
利用采样得到的轨迹片段来估计梯度，并使用梯度上升法来优化策略

基于时序差分的策略梯度法：Actor-Critic 算法

使用下一时刻状态的价值函数来估计当前状态的价值函数，而不是使用整个片段的反馈值
$R + γ V_{π_{θ}} (s^{'})$
和 DQN 一致，计算 q 值时使用另一套参数 w 进行计算

03 Q-Learning

Q-Learning 算法流程

初始化 $q_{π}$ 函数
循环
- 初始化 s 为初始状态
- 循环
  - $a = {argmax}_{a^{'}} q_{π} (s, a^{'})$
  - 执行动作 $a$ , 观察奖励 $R$ 和下一个状态 $s^{'}$
  - 更新 $q_{π} (s, a) \leftarrow q_{π} (s, a) + α [R + γ max_{a^{'}} q_{π} (s^{'}, a^{'}) - q_{π} (s, a)]$
  - $s \leftarrow s^{'}$
- 直到 s 是终止状态直到
$q_{π}$ 收敛

Example

Pasted image 20250530134531.png
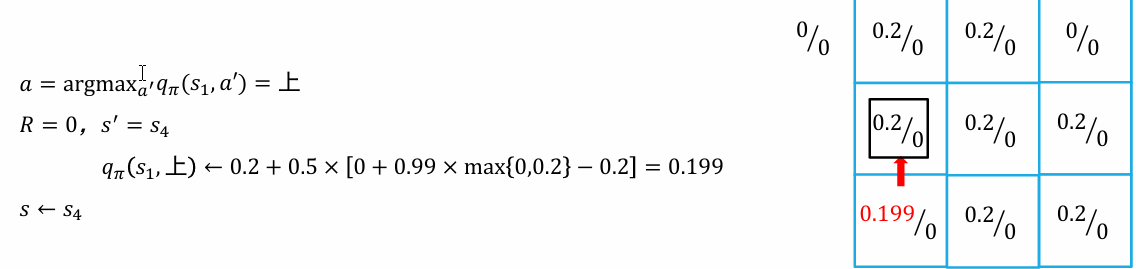
Pasted image 20250530134612.png
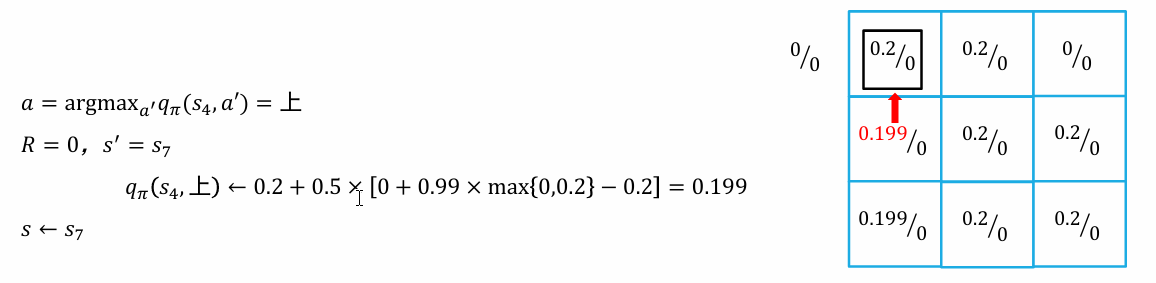
Pasted image 20250530135029.png
Pasted image 20250530135116.png
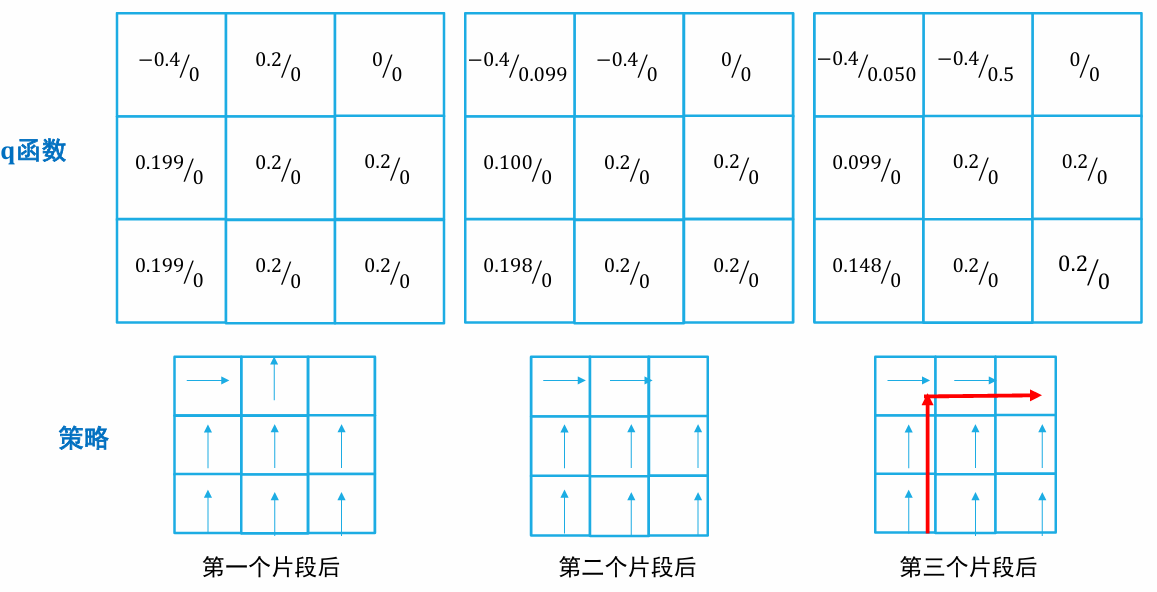
Pasted image 20250530135301.png

探索（exploration）与利用（exploitation）的平衡

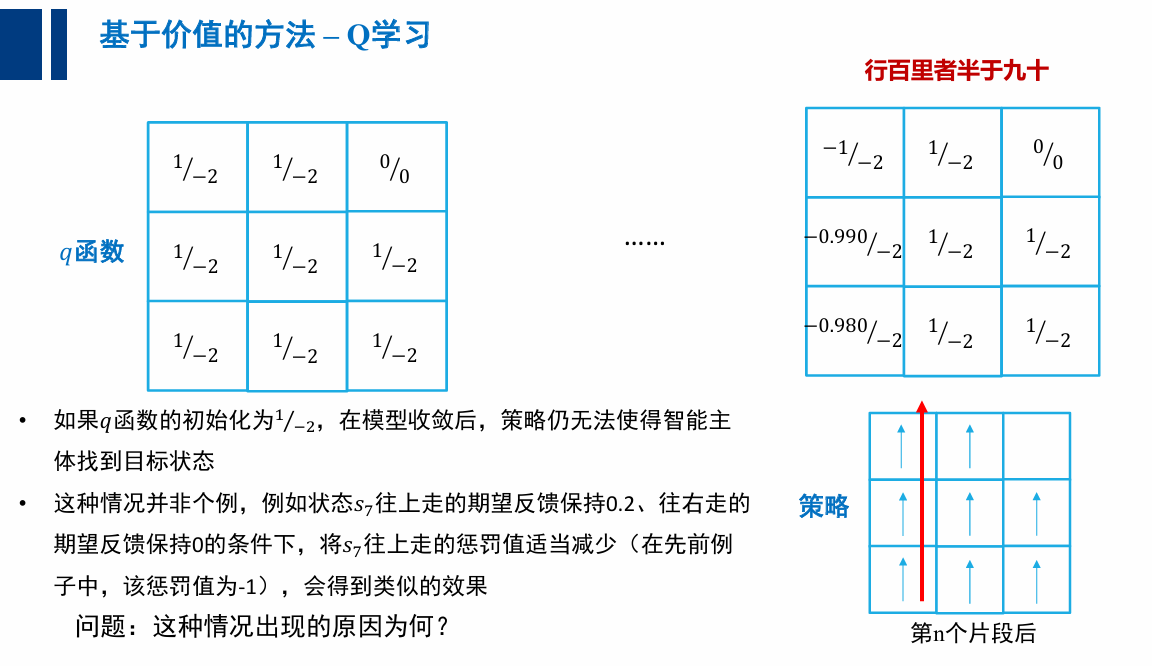
为何 Q 学习收敛到非最优策略？

算法中只有利用没有探索
(特定的 q 初始 q 函数，会让策略无法改变其轨迹)

大体上利用，偶尔探索👇
$ϵ$ 贪心（ $ϵ$ -greedy）策略：

ϵ - g r e e d y_{π} (s) = {\begin{cases} {argmax}_{a} q_{π} (s, a), & 以 1 - ϵ 的概率 \\ 随机的 a \in A, & 以 ϵ 的概率 \end{cases}

加上

ϵ

贪心（

ϵ

-greedy）策略后的 Q-Learning

初始化 $q_{π}$ 函数
循环
- 初始化 s 为初始状态
- 循环
  - $a = ϵ - g r e e d y_{π} (s)$
  - 执行动作 $a$ , 观察奖励 $R$ 和下一个状态 $s^{'}$
  - 更新 $q_{π} (s, a) \leftarrow q_{π} (s, a) + α [R + γ max_{a^{'}} q_{π} (s^{'}, a^{'}) - q_{π} (s, a)]$
  - $s \leftarrow s^{'}$
- 直到 s 是终止状态直到
$q_{π}$ 收敛

Example

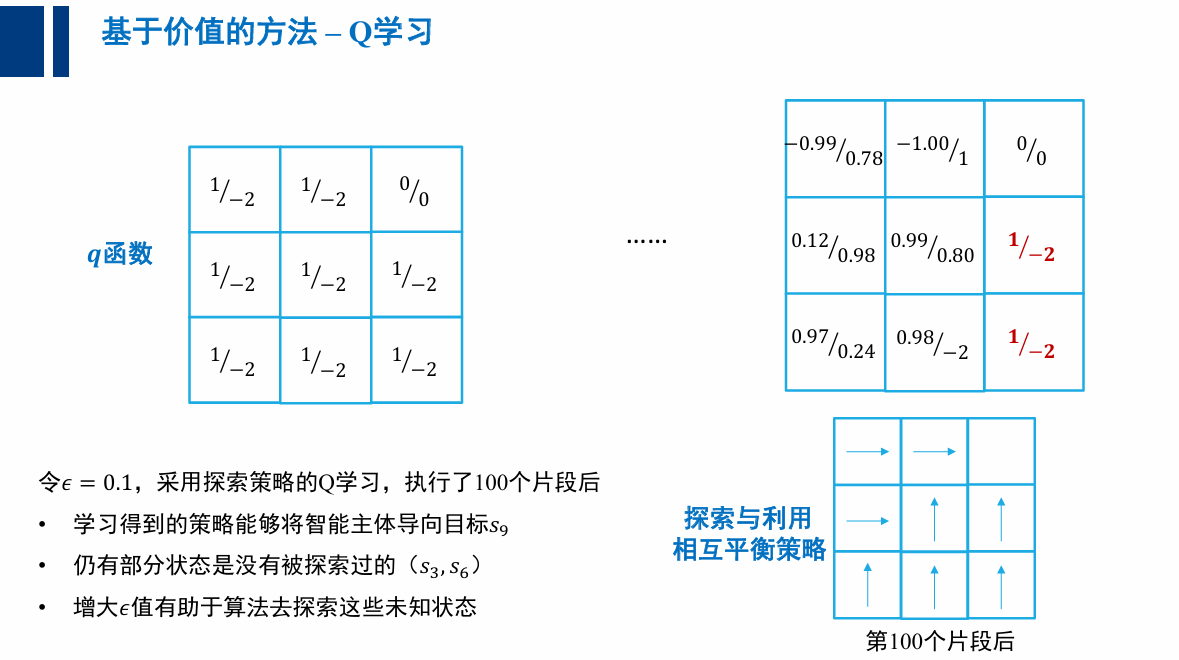
Pasted image 20250530141250.png|475

04 深度强化学习

深度 Q 学习

状态数量太多时，有些状态可能始终无法采样到
状态数量无限时，不可能用一张表 (数组) 来记录𝑞函数的值
👉 将𝑞函数参数化（parametrize），用一个非线性回归模型来拟合𝑞函数，例如 (深度) 神经网络

伪代码：深度 Q 学习

初始化 $q_{π}$ 函数的参数 $θ$
循环
- 初始化 s 为初始状态
- 循环
  - 采样 $a \sim ϵ - g r e e d y_{π} (s; θ)$
  - 执行动作 $a$ , 观察奖励 $R$ 和下一个状态 s'
  - 损失函数 L $(θ) = \frac{1}{2} {[\begin{matrix} R + γ max_{a^{'}} q_{π} (s^{'}, a^{'}; θ) - q_{π} (s, a; θ) \end{matrix}]}^{2}$
  - 根据梯度 $\partial L (θ) / \partial θ$ 更新参数 $θ$
  - $s \leftarrow s^{'}$
- 直到 s 是终止状态
指导 $q_{π}$ 收敛

两个不稳定因素：

相邻的样本来自同一条轨迹，样本之间相关性太强，集中优化相关性强的样本可能导致神经网络在其他样本上效果下降
在损失函数中，𝑞函数的值既用来估计目标值，又用来计算当前值。现在这两处的𝑞函数通过𝜃有所关联，可能导致优化时不稳定

经验重现 Experience Replay

将过去的经验存储下来，每次将新的样本加入到存储中去，并从存储中采样一批样本进行优化
解决了样本相关性强的问题
重用经验，提高了信息利用的效率

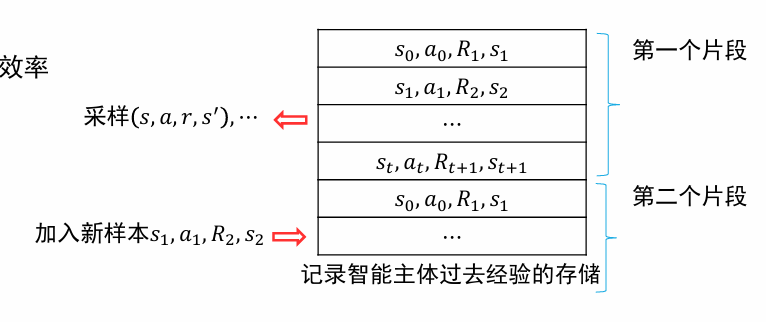
目标网络 Target Network
$$\frac12[R+\gamma\max_{a^{\prime}}\boxed{q_\pi (s^{\prime}, a^{\prime};\theta^{-})}-q_\pi (s, a;\theta)]^2$$

损失函数的两个𝑞函数使用不同的参数计算
用于计算估计值的 $q$ 使用参数 $θ^{-}$ 计算，这个网络叫做目标网络
用于计算当前值的 $q$ 使用参数 $θ$ 计算
保持 $θ^{-}$ 的值相对稳定，例如 $θ$ 每更新多次后才同步两者的值

θ^{-} \leftarrow θ

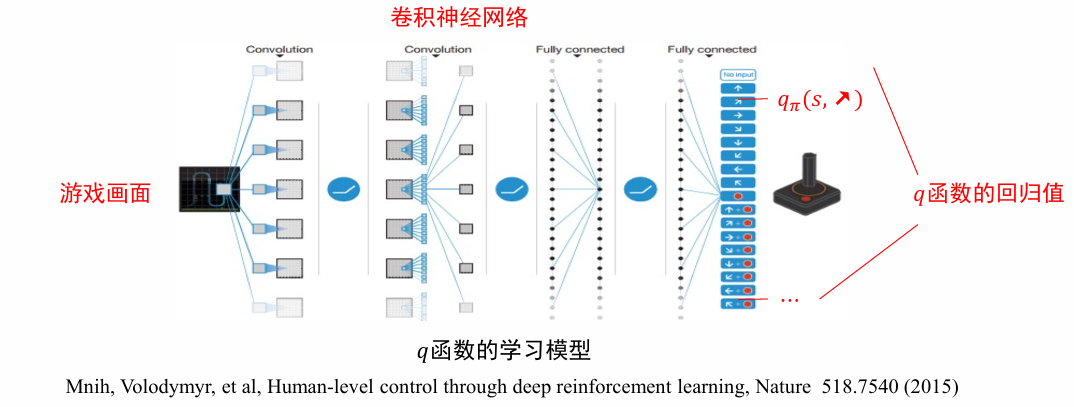
Tips of Q-Learning

考试不作要求

一些科研的经验分享

05 多智能体强化学习

考试不作要求

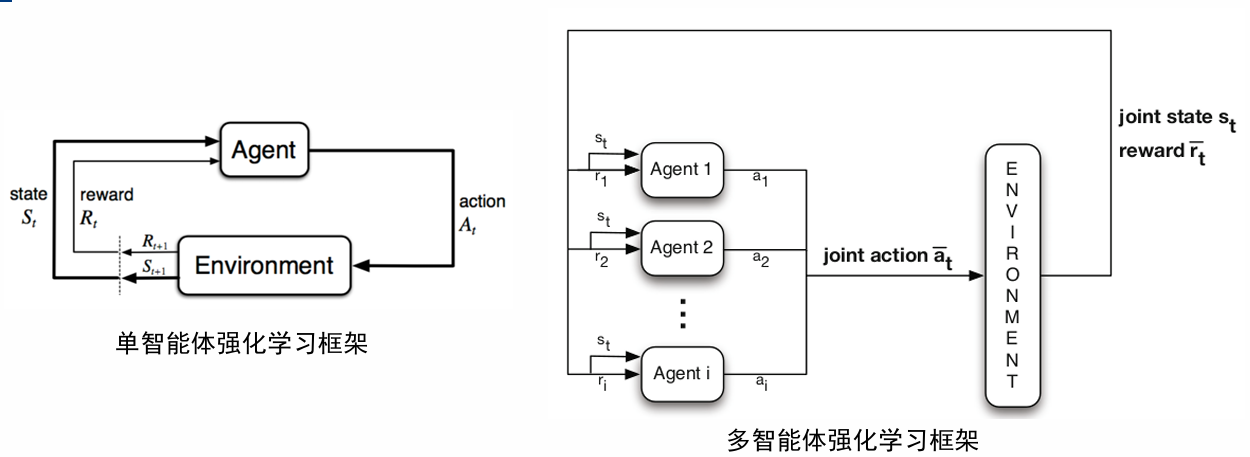
两个问题：

多智能体信用分配问题 (Credit Assignment)
- 当只存在 Global reward 时，如何为每个智能体分配 Reward or Value function
多智能体通信学习问题 (Communication Learning)
- 每个智能体如何与其他智能体进行高效的交流

沙普利值

Pasted image 20250530144043.png|450
Pasted image 20250530144058.png|450
Pasted image 20250530144112.png|450